A Tropical Geometry Framework for Non-Hermitian Systems
In the realm of quantum mechanics, the principle of hermiticity – which governs isolated, closed systems – has long been fundamental, ensuring that systems possess real observables and conserve probability. In recent years, researchers have begun exploring non-Hermitian systems where such requirements break down due to inflow or outflow of energy and matter from the surroundings. Unlike traditional closed cases, these unconventional systems exhibit counterintuitive behaviours and open up new possibilities for manipulating and controlling light, sound, and even quantum states.
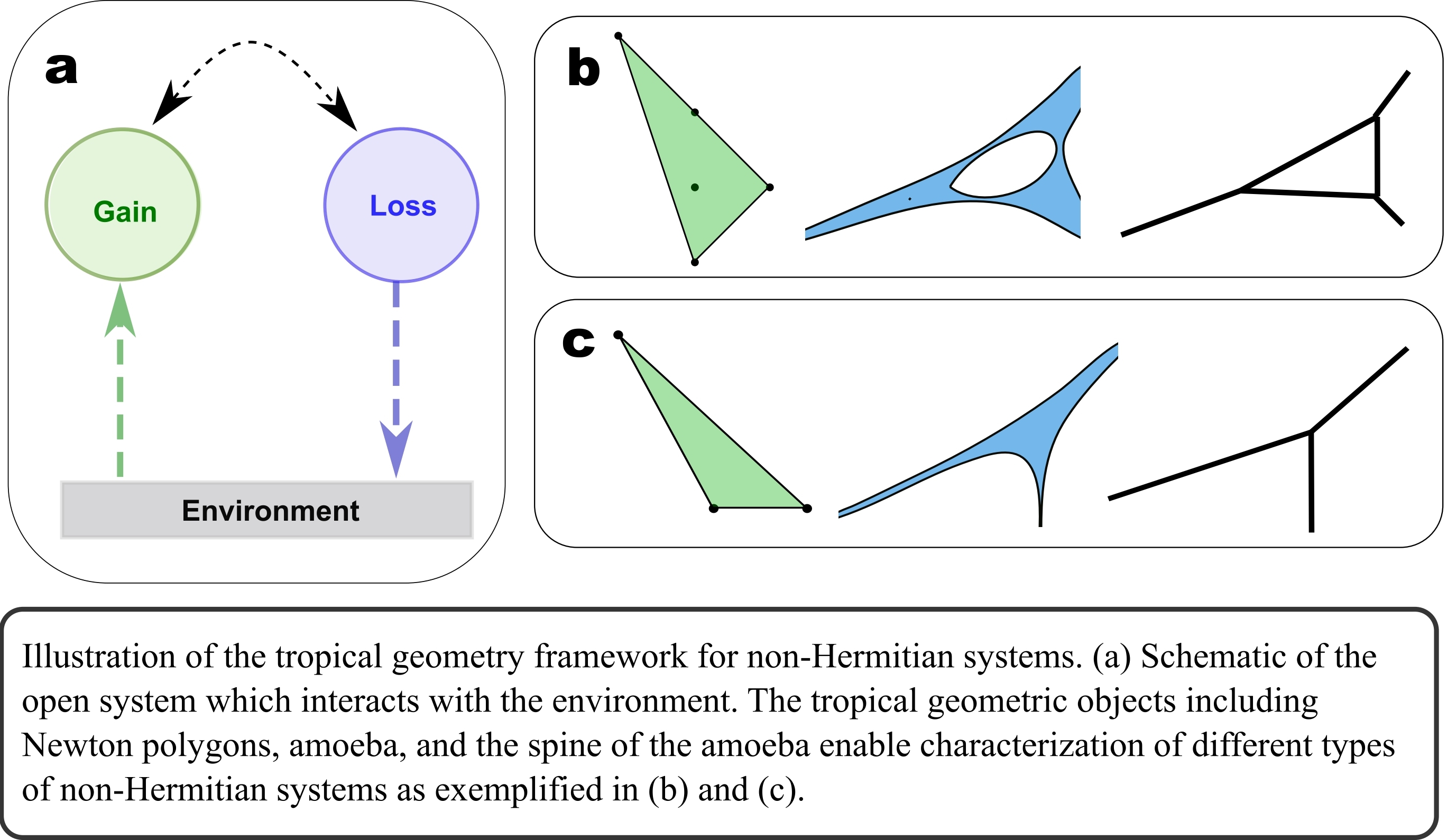
Mathematics has long been a powerful tool for understanding the natural world. One fascinating branch of mathematics is tropical geometry, which, remarkably, has not only found applications in geometry but also in diverse fields such as physics, number theory, genetics, economics, optimisation theory, and computational biology.
Now, a team of researchers at Solid State and Structural Chemistry Unit, IISc, including Ayan Banerjee, Rimika Jaiswal and Awadhesh Narayan, along with Madhusudan Manjunath at IIT Bombay, have introduced a new tropical geometric framework to understand and characterise non-Hermitian systems.
In this study, the researchers discovered a surprising connection between the seemingly different fields of non-Hermitian systems and tropical geometry. The researchers showed that the concepts that arise naturally in the tropical setting are ideally suited to understand the defining features of non-Hermitian systems. Using these ideas leads to a considerable simplification of calculations required to understand such complex physical systems.
The researchers’ proposed framework also opens up avenues for further exploration. The framework’s natural treatment of disorder – inevitable in any real system – suggests potential in identifying optimal conditions to realise non-Hermitian effects in experimental setups. The study is also expected to lead to a greater synergy between mathematics and non-Hermitian systems.

REFERENCE:
Ayan Banerjee, Rimika Jaiswal, Madhusudan Manjunath, and Awadhesh Narayan, Proceedings of the National Academy of Sciences (2023).
LAB WEBSITE:
https://sites.google.com/site/awadheshnarayan00/Home
https://twitter.com/anarayan_





