Resolving a century old debate on entropy in isolated systems

Image: Ananth Govind Rajan
Miniaturised systems consisting of a few atoms, molecules, or electrons are increasingly technologically relevant. However, the theory available to describe the statistical thermodynamics of such systems, when isolated from their surroundings, faced several challenges. For one, it could not correctly predict when small isolated systems would exhibit negative absolute temperature, a signature of systems with an upper bound on the system energy. Such situations arise in important applications such as lasers and nuclear spin systems, when highly energetic system levels are more populated than lower energy levels, leading to a reduction in entropy with an increase in energy.
Over the past 120 years, an ongoing debate in the field of statistical mechanics was whether the volume entropy of a system – espoused by Gibbs, Hertz, and others – is more applicable or the surface entropy – supported by Boltzmann, Planck, and others – is better suited to describe small isolated systems. On the one hand, Gibbs’ definition based on the volume of the allowed states disallowed negative absolute temperatures, in disagreement with experiments. On the other hand, the definition attributed to Boltzmann, based on the surface area of the allowed states, predicted such temperatures even when they are physically unrealisable.
To solve this conundrum, recent work by Ananth Govind Rajan, Assistant Professor in the Department of Chemical Engineering at IISc, published in The Journal of Physical Chemistry Letters, has proposed a modification to surface entropy, which preserves the beneficial properties of the volume and surface entropy definitions, thus effectively resolving the debate.
The new entropy definition for isolated systems is centered on the use of a relative energy window for allowable system energies, motivated by the Heisenberg uncertainty principle and eigenstate thermalisation in quantum mechanics. It thereby enables the calculation of the temperature versus energy relationships accurately for several example systems, thus demonstrating its utility for describing the statistical thermodynamics of small, isolated systems. Notably, in addition to enabling correct predictions for miniaturised systems, where the Boltzmann and Gibbs entropies faced challenges, the proposed entropy definition agrees with the original Boltzmann entropy for macroscopic systems.

The proposed entropy considered a relative energy window ϵr to determine the number of states at a given energy E, thus ensuring T > 0 K for unbounded energy systems and allowing T < 0 K for bounded energy systems
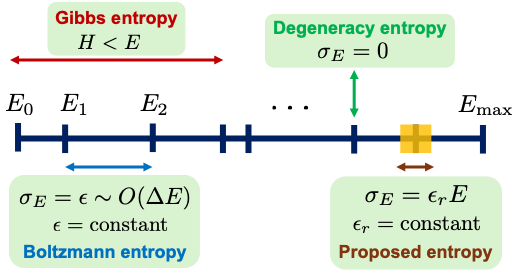
Various entropies that can be defined for isolated systems and the states (w) that they consider (indicated by double-ended arrows) in applying the formula S = k log w to calculate the entropy of the system
Images reproduced with permission from the American Chemical Society (Govind Rajan, A. Resolving the Debate Between Boltzmann and Gibbs Entropy: Relative Energy Window Eliminates Thermodynamic Inconsistencies and Allows Negative Absolute Temperatures. J. Phys. Chem. Lett. 2024, 15, 9263–9271.)

Ananth Govind Rajan with his research group
REFERENCE:
Govind Rajan A, Resolving the Debate Between Boltzmann and Gibbs Entropy: Relative Energy Window Eliminates Thermodynamic Inconsistencies and Allows Negative Absolute Temperatures, Journal of Physical Chemistry Letters (2024).
https://pubs.acs.org/doi/10.1021/acs.jpclett.4c02400
LAB WEBSITE:
https://agrgroup.org







